Benzetilmiş tavlama ya da benzetimli tavlama algoritması, optimum (eniyileme) problemi için tasarlanmış olasılıksal yaklaşımlı bir algoritmadır. Benzetilmiş tavlama en iyi çözümün en kısa zamanda üretimini hedefler. Bu sebeple, özellikle matematiksel modellerle çözülmesi maliyetli olan kombinasyonel optimum problemlerinde kullanılır[1].
Benzetimli tavlamanın çalışma prensibi metalürjideki ısıl işlemden gelmektedir. Metalurjide tavlama, malzemeyi belirli bir süre (tavlama sıcaklığına kadar) ısıttıktan sonra, yavaş yavaş soğutmaktır. Tavlama malzemeyi rahatlatmak, yumuşatmak ve iç yapıyı daha kullanılabilir hale getirmek için yapılan ısıl işlemlerin geneline verilen isimdir.
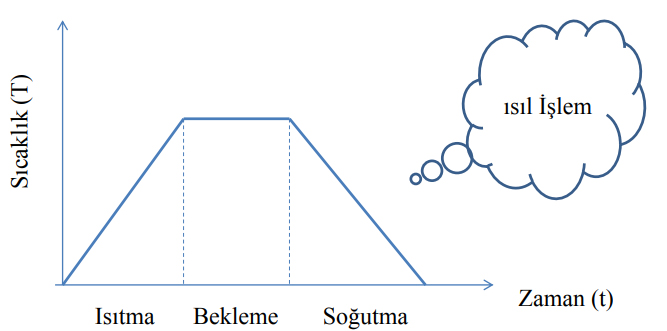
Isıl işlem, bir katının sıcaklığının belirli bir maksimum dereceye kadar artırılarak tekrar azaltılması işlemidir. Maksimum sıcaklıkta kristalin tüm molekülleri, kendilerini rasgele olarak sıvı faza ayarlar. Sonra, erimiş kristalin sıcaklığı kristal yapı soğutuluncaya kadar düşürülür. Soğuma uygun şekilde yapılırsa kristal yapı çok düzenli olur[2].
Şekil.1. Isıl işlem Prosesi[2]
Algoritmanın mantığını anlayabilmek için bir örnekle pekiştirelim. Bu örnekte, en alçak noktasını aradığımız bol delikli bir golf sahası olsun. Eğer sahanın eğimi yönünde ilerlemek gibi basit bir yöntem kullanırsak yüksek olasılıkla deliklerden birinde takılabiliriz. Bu takılmayı önlemek ve yerel minimum’dan kurtulmak için şöyle bir işlem yapıyoruz: Sahaya bir top koyup araziyi olduğu gibi sallamaya başlıyoruz. Top arada bir deliklere girse de sürekli salladığımız için delikten çıkıyor ve yerel minimum’dan kurtuluyor. Zamanla sallama hızımızı yavaş yavaş azaltıyoruz. Tamamen durduğumuzda ise topumuzun sahanın en alçak noktasında (genel minimum) ya da yakın bir yerlerde olduğunu farz ediyoruz.
Gerçek dünyadaki katı cisimlerde de durum bu örnektekine benzer. Örnekteki sallama hareketi cisimlerin sıcaklığına karşılık gelmektedir. Bir gazı soğuturken atomlar bir süre sonra nasıl ki periyodik aralıklarla dizilip potansiyel enerjiyi minimize ediyorlar ise (kristalleşme) biz de aynı yöntemi kullanarak enerjiyi değil kendi tanımladığımız bir fonksiyonu minimize etmeye çalışıyoruz.
Bölgesel en iyi çözümlere (local optimum) takılmamak için bu en iyi yöntemlerden biridir. Soğutma işlemi bu algoritmada daha iyi sonuçların bulunmasını sağlayacak yeni komşu çözümlerin üretilmesini sağlayan üstel (exponential) bir ifadedir[3].
Kullanılan Alanlar
- Elektronik devre tasarımı,
- Görüntü işleme,
- Yol bulma problemleri,
- Seyahat problemleri,
- Malzeme fiziği benzetimi,
- Kesme ve paketleme problemleri,
- İş/akış çizelgeleme ve benzeri pek çok problemin çözümümde kullanılabilir.
Benzetimli Tavlama Algoritması
Şekil.2. Benzetimli Tavlama algoritması[3]
Bu algoritmanın özelliği: T’nin¸ çok büyük değeri için başlayan hareket uzaydaki birçok noktayı gezer. Bir sonraki harekette T belli bir miktar azaltıldığında hareket yine uzayın büyük ama bir önceki harekete göre daha küçük bir bölümünde ve bir önceki harekette bulunan minimum noktasından başlayarak gerçekleşir. Eğer bu başlangıç noktası global minimum değilse program hareketi sırasında bir önceki hareketten biraz düşük olan T sayesinde bir çok yerel minimumu aşacak ve global minimumu bulacaktır. Belli bir T’den daha düşük değerdeki T’ler için ise hareket artık uzayın küçük bir kısmında ve hep global minimum civarında olacak böylece program sonlandığında global minimumu veren iyi bir hassasiyet ile belirlenmiş olacaktır[3,4,5].
Bu video, benzetilmiş tavlama optimizasyon algoritmasının bir çalışmasını gösterir.
Referanslar
[1] Benzetilmiş tavlama, https://tr.wikipedia.org/wiki/Benzetilmi%C5%9F_tavlama, (11.04.2020, hala çalışmakta)
[2] AYDIN, I., Tavlama Benzetimi Algoritması, http://web.firat.edu.tr/iaydin/bmu579/bmu_579_bolum7.pdf (11.04.2020, hala çalışmakta)
[3]Cayıroglu, I., İleri Algoritma Analizi http://www.ibrahimcayiroglu.com/Dokumanlar/IleriAlgoritmaAnalizi/IleriAlgoritmaAnalizi-8.Hafta-IsilislemAlgoritmasi.pdf (11.04.2020, hala çalışmakta)
[4]S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi, “Optimization by Simulated Annealing,” Science, vol. 220, no. 4598, pp. 671-680, 1983.
[5] N. Metropolis, A. W. Rosenbluth, M. Rosenbluth, A. H. Teller, and E. Teller, “Equation of State Calculations by Fast Computing Machines,” J. Chem. Phys., vol. 21, pp. 1087-1092, 1953.